Clase 3

Figuras Tridimensionales

Habilidades específicas

1. Reconocer en figuras tridimensionales diversos elementos como caras, aristas, vértices.
2. Establecer relaciones entre los diversos elementos de figuras tridimensionales: vértices, caras y aristas, rectas y segmentos paralelos, perpendiculares, planos paralelos y perpendiculares.

Problema inicial: 

Miguel compró una caja fuerte en forma de cubo, él guardó sus ahorros y al cerrar la caja escribió una letra mayúscula en cada esquina como se muestra en la siguiente figura:

Decidió que la combinación de la caja fuerte sería de cuatro dígitos.
El primer dígito corresponde al número de esquinas de la caja.
Como segundo dígito tendría el número de caras de la caja fuerte y como dígitos finales se tendría al número de bordes que tiene la caja fuerte.
 
¿Cuál es la combinación para abrir la caja fuerte de Miguel?

Déjalo en los comentarios y explícanos como halló la solución

Figuras tridimensionales

Antes de introducir el mundo tridimensional, es de suma importancia tener claro algunos conceptos de la geometría plana tales como: puntos, segmentos, rectas, planos, rectas paralelas y perpendiculares, entre otros que son tomados en cuenta en esta sección.

Para comenzar con el tema de figuras tridimensionales, es necesario acercarte a una definición muy importante.

Los cuerpos geométricos tridimensionales:

Los cuerpos geométricos tridimensionales son aquellos que ocupan un volumen en el espacio desarrollándose por lo tanto en las tres dimensiones de alto, ancho y largo; y están compuestos por figuras geométricas.

Aprendamos los siguientes elementos de una figura tridimensional.

a.       Vértice. 

Son los puntos donde concurren cada una de las caras de la figura. Se representan con letras mayúsculas además tres caras coinciden en un mismo vértice.

Ejemplo 1: 

Ejemplo2: 

b.      Caras.

Las caras de una figura tridimensional son cada uno de los polígonos que limitan a la figura. Las bases también cuentan como caras.

Ejemplo 1:

Ejemplo 2:

c.       Aristas.

Las caras de una figura tridimensional son cada uno de los polígonos que limitan a la figura. Las bases también cuentan como caras.

Ejemplo 1: 

Ejemplo 2: 

Veamos el siguiente vídeo para tener claro estos conceptos.

Por otra parte el número de vértices, de caras y de aristas va a depender del cuerpo tridimensional a tratar por ejemplo:

Figura tridimensional	N° de caras	N° de aristas	N° de vértices
CUBO	6   Formado por: 6 cuadrados	12	8
PIRÁMIDE DE BASE TRIANGULAR	4   Formado por: 4 triangulos	5	4
PIRÁMIDES DE BASE CUADRADA	4   Formado por: 3 triángulos 1 cuadrado	8	5
PRISMA DE BASE TRIANGULAR	5   Formado por: 3 rectángulos 2 triángulos	9	6
PRISMA DE BASE RECTANGULAR	6   Formado por: 6 rectángulos	8	12

¡Pensemos!

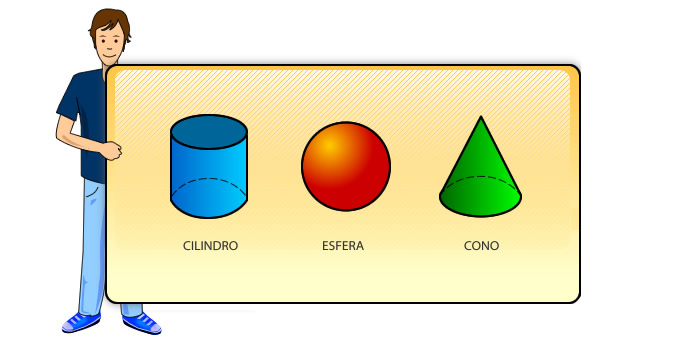
¿Que pasa con figuras tridimensionales como la esfera, el cilindro y el cono?

Estas figuras son muy peculiares.

Por ejemplo, la esfera no tiene aristas ni vértices, solo posee una cara, mientras que el cilindro no tiene vértices pero posee tres caras, dos circunferencias y un rectángulo (compruébalo con una hoja de papel) y por último el cono sólo posee un vértice y posee como base una circunferencia.

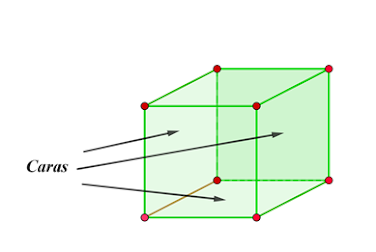
¿Sabía usted que existen más elementos en una figura tridimensional?

 

Observe atentamente la siguiente imagen que corresponde a un prisma rectangular.

 

 

Con base en la figura anterior, conteste las siguientes preguntas:

  1.   ¿Es posible que el prisma tenga rectas que sean paralelas? y si es así cite un par de rectas paralelas.

2.   ¿Cuáles aristas comparten un mismo vértice?

 

3.    Escriba un par de rectas perpendiculares.

 

4.   ¿Cuántas caras tiene el prisma rectangular?

 

5.   Cite dos caras que sean perpendiculares.

Previamente, hemos aprendido muchos conceptos geométricos que ahora son visibles en las figuras tridimensionales, para ello veamos el siguiente ejemplo.

 

Ejemplo #1

 

 

De la figura anterior podemos obtener la siguiente información:

Como puedes notar, la definición de paralelismo y perpendicularidad no cambia en figuras de tres dimensiones.

Observación:  Usted puede buscar dentro de la misma figura otras rectas, segmentos y planos que sean paralelos y perpendiculares.

Otro dato a considerar es que existen figuras tridimensionales que no tienen rectas, aristas y planos que sean paralelos o perpendiculares, por ejemplo la pirámide de base triangular, la esfera, el cono, entre otros.

Pero hay muchísimas más figuras que si poseen estos elementos.

 

Observemos el siguiente vídeo para repasar estos conceptos de la mejor manera:

Apliquemos nuestro conocimiento.

¿Será que tu habitación posee rectas y segmentos paralelos e incluso planos que son paralelos y perpendiculares? Si su respuesta es afirmativa, considere las paredes  y el piso como planos, noten que una pared con el piso forman don planos perpendiculares. Consideremos el piso, observen que hay muchos segmentos que son paralelos y algunos también perpendiculares.

Compruébalo y te darás cuenta que la geometría tridimensional está presente en nuestra vida cotidiana.